Kuidas tekitada 10-12-aastastes vaimustust programmeerimise ja matemaatika vastu? Jagan lugu kuidas programmeeritav taskuarvuti mind 1980ndatel ümber sõrme keeras, et inspireerida teisigi kogemusi ja mõtteid jagama.
Kokkuvõte:
- Esimene asi oli leida lihtsad ja lõbusad ülesanded. Et saaks ka sõbrad vaimustuma.
- Teiseks: lahe kui sain progemisega lahendada igapäevaseid probleeme – taas, et oleks huvitav ja saaks teistega jagada.
- Ägedad olid matemaatilised seiklused kui “aaretejaht”. Neisse võis ennast tundideks unustada.
Kalkulaator
Õppisin väikeses külakoolis. Klassis 15 last. Matemaatika õpetamise tase oli meil selline maakooli “tubli Eesti tavaline”. Kes jõudis enam, sai õpetajalt lisaülesandeid. Kes vähem, sellega töötati rohkem.
12-aastaselt sain vanaisalt laenuks Elektronika B3-34 kalkulaatori. See erines sovhoosi raamatupidajate omadest, mis olid kui raamatusuurused kassaaparaadid. Vanaisa taskuarvuti oli väiksem. Rohkemate nuppudega. Võõrapärane nagu kosmoselaeva paneel. Võrratu vidin. Salvestas kuni 8-kohalisi arvusid 14 mälupessa ning võimaldas ilma täiendavaid nupuvajutusi nõudmata käia läbi kuni 98 rea ulatuses kasutaja poolt ette antud käsklusi.

Tänases mõõtkavas oli ta muidugi tiguaeglane. Igaks operatsiooniks kulus pool sekundit, ehk 1,000,000,000 korda rahulikum kui tänane taskutelefon.
See aeglus lõi samas rütmi. Ühendasid juhtme. Lülitasid sisse. Lugesid raamatust juhendit ja sisestasid programmkoodi. Mällu muutujad. Lõpuks käivitasid ja ootasid vilkuva ekraani ees kuni tulemus käes. Vahetasid muutujaid. Kordasid ja proovisid uuesti. Kui arvuti välja lülitasid või aku tühjaks sai, siis programm mälust kadus. Tuli otsast alata.
Kogu arvuti kasutamise rituaal oli iga kord nagu oma kätega leiva küpsetamine. Teed ja ootad ja kui tulemus valmis, siis lõhnab hästi.
Raamatud ja näited
Minu huvi tõmbas käima kaks raamatut. Tomass Romanovskise “Taskuarvutist nii ja teisiti” ja Gennadi Slavini “Programmeerimine programmeeritaval mikrokalkulaatoril «Elektroonika Б3-34»“. Neis oli kõike, mida noor huviline vajas. Mängud. Katsed. Nipid, millega kooli matemaatikaülesandeid lihtsustada.

Raamatu illustratsioonid
Kirjeldan vasakpoolset raamatut. Romanovskise raamatu visuaalne lahendus oli selle aja kohta väga äge. Illustratsioonidel olid minuvanused tüdrukud ja poisid. Nad paistsid isegi keeruliste teemade juures keeruliste töövahendite ja arvutuskäikudega kenasti hakkama saavat. Kui nemad said, siis ei tekkinud endal kordagi tunnet, et midagi oleks liiga keerulist. Pigem ikkagi, et “Hmm. Korra süvenen!” ja seejärel, et: “Vau, kui äge – see on ju imelihtne!”
Mõistata arv
Esimene mäng. Mõte, et kalkulaatori vahemälu kasutades saab mängida pikkade arvude mõistatamise ning liitmise-lahutamise mängu on iseenesest geniaalselt lihtne: üks laps sisestab arvu. Teine mõistatab, vajutab võrdusmärgi ja ekraanil näeb iga kord vastusena et kas peab suurendama või vähendama enda pakkumist kuni ekraanil on lõpuks null = õige vastus!
Ilmselt pole tegemist meelelahutusega pikkadeks tundideks, aga soojendusharjutuseks päris hea. Kui võtta alustuseks väiksed arvud, võib seda mängida juba eelkoolieas. Täna on seda asendamas kümned peastarvutamise äpid, kahoot ja isegi mitme kasutaja üheaegset võistlemist lubav 99Math, mis lisavad taimeri, mõõdavad skoori ja peavad edetabelit. Niisiis praegused lahendused tunduvad igal juhul ägedamad. Kuidas teistele tundub?

Numbrid on ju tagurpidi tähed!
Teine mängude grupp eeldab, et kalkulaatori font oleks piisavalt kandiline. Sel juhul on taskuarvutit tagurpidi keerates võimalik numbritega kirjutada igasuguseid sõnu. Puberteediealisi paneb see tegema kelmikaid katsetusi. Kirjuta number arvutisse ja loed …:
73533 = EESEL
7707 = LOLL
Romanovskis leidis, et vahva oleks arendada sellist keele-numbrite kombinatsiooni edasi. Ja ühtäkki ei ole arvuti tagurpidi keeramine enam teismeliste kujuneva huumorimeele väljendus. Selleks saab hoopis nutikas mõistatus, mis soodustab tõsist õppimist üle erialade piiride. Tee arvutus ja saad teada … :
Milline ese on:
muusikariist = 7 * 11 / 0.025
kaunistus = sqrt(117649)
koduloom = 16^4 + 7997
Kuidas on inglise keeles:
jalanõu(i.k.) = 203 * 2145 / 11 * 13
mesilane(i.k.) = sqrt(152^2 + 302^2 - 8^2)
Saksa keeles:
järv(s.k.) = (65428 - 2783) / 187
õli(s.k.) = (1/0.25 + 1/0.125) * 60 + 10
Või:
Kõrbes käis lahing kahe ruudukujulise maatüki pärast. Esimese serva pikkus oli 5324m ja teisel 6537m. Leides maatükkide pindalade summa saad teada, kes sellest lahingust võitjana väljus.Alltoodud fotodelt võib vaadata neid numbri-tähe kombinatsiooni ülesandeid täpsemalt. Mida arvate – kas selliste mõistatuste lahendamine võiks praegu kedagi kõnetada?
Duell siiliga
Minu ja mu klassivendade lemmikmänguks oli “Duell siiliga” (tuntud kui: “Nim“). Mängu alustatakse näiteks 18 sammu kauguselt. Tuleb astuda arvutiga vaheldumisi üksteise suunas 1..3 sammu. Viimase sammu astuja võidab ja saab virtuaalsel duellil vastast torgata.
Korraldasime omavahel koolis siili duelli turniire. Peatselt nuputasin välja eduka strateegia üritades dešifreerida arvutisse sisestatud programmi. Mängu võiduks oli ju tarvis teha viimased sammud. Kui mõlemad osapooled võisid astuda 1..3 sammu, siis alustuseks tuli jõuda 4ga jagatava arvuni (nt 16) ja seejärel tuli edukaks strateegiaks vastasele vastu astuda alati:
Minu käik = (4 - vastase käik)Seda loogikat mõistes polnud mulle enam vastast. Mõne aja pärast said ka teised sellest aru ja siis üritasime avastastada viise arvutit üle kavaldada. Näiteks võisid kohe esimese käiguna sisestada kogu liikumistee pikkuse ja said ainsa liigutusega reegleid rikkudes arvutile pähe teha. Natuke nagu häkker juba. 🙂
“Siili duelli” võlu oli see, et see oli loomult sotsiaalne mäng, milles võisid põhimõtteliselt mõlemad võita, aga kus nutikus ja ette mõtlemine andsid lõpuks siiski edumaa. Mida arvate, et kuidas see mäng praegu lapsi kõnetaks?
Kui kaugel on silmapiir?
Järgmiseks oli ette seal mitmeid lihtsaid arvutusi. Näiteks kuidas mõõta silmapiiri kaugust silmade kõrgusel, vaatlustornis või lennukis. Kui kahe lapsega joonistatud juhendit siin all lehel lähemalt vaadata, siis selgub, et tegemist on lihtsa valemiga ja väga illustratiivselt esitatud selgitusega.
silmapiiri kaugus kilomeetrites = sqrt(12.74 * kõrgus meetrites)Ruutjuur maa läbimõõdu konstandi ja maapinna kõrguse korrutisest annab tulemuse, mida on võimalik kalkulaatoris kirjutada 4 sammust koosnevaks koodijupiks, millest sai isegi 12-aastane aru, et seda korduvalt taaskasutada.
Kuidas tundub – minu jaoks oli see vahend, mis aitas toita sõpradega ühist uudishimu ja küsida: “Kas teadsid, et …” ning siis ühiselt vastust välja arvutada. Kas selline lähenemine ka praegu toimiks?

Saa teada oma biorütmid
Tänaseks on biorütmide analüüsimine kuulutatud pseudoteaduseks. Natuke nagu “matemaatikaga palistatud astroloogia”, aga 80ndatel oli see populaarne. Fantaasia lendama laskmiseks oli huvitav ülesanne konstrueerida kalkulaatori abil vastavalt 23, 28 ja 33-päevalisi sinusoide, mis pidid eeldatavasti vastama füüsilise, emotsionaalse ja intellektuaalse rütmi faasideks.
Selleks tuli kõigepealt välja arvutada oma vanus päevades. Alltoodud valem näitas kui kaugel oli mingi päev 31. detsembrist 1899.a. Käivitasid programmi kaks korda ja said teada oma sünnikuupäeva ja hetkel käes oleva kuupäeva vahe päevades:
S = INT((22 - kuu number) / 10);
N = INT((aasta number - 1899 - S) * 365.25) + INT((12 * 2 + kuu number - 14)) * 30.59) + 29 + päeva numberKui vanus päevades oli teada, siis tuli see jagada vastavalt 23, 28 ja 33ga. Teadsidki, et kuidas sul keha, tunded ja mõistus töötasid. 🙂 Saadud jäägi põhjal oli võimalik panna endale lõbusalt “diagnoos” ja kuulutada sõbrale, et täna on sul kõik miinuses.
Kas pseudoteaduse kultiveerimine oleks pigem eetiliselt taunitav või oleks selliste kõverate välja arvutamine ja ühiselt joonistamine kellegi jaoks ka õpetlik ja huvitav?

Igapäevaelu matemaatika näited
Seejärel läheb raamat üha edasi, pakkudes välja erinevaid ideid ja näidiseid, mille abil on võimalik välja arvutada, sarnaste lühikeste valemitena:
- Missugune on sinu keha rasvaprotsent sõltuvalt sinu pikkusest ja kaalust,
- mõõta inimese keha proportsioone lähtuvalt kuldlõikest,
- kui pikk on jalgratta pidurdustee sõltuvalt kiirusest,
- modelleerida kivi viskamise kaugust sõltuvalt algkiirusest ja jõust,
- kuidas joonestada paberilehele erinevaid võrdkülgseid hulknurki – nii et kõikide tippude asukohad oleksid õigesti välja arvutatud,
- mõõta, et kui kaugel on kaks linna üksteisest linnulennult kui on teada geograafilised koordinaadid,
- genereerida juhuslikke arvusid, et arvuti oleks täringu asemel.
Mõned näited nendest lehekülgedest taas alltoodud fotodel. Kõik lihtsalt esitletud – valem olemas, programmi struktuur ette antud ja selgitus kõrval, et saaks ise kohe eksperimenteerida ja sõbraga läbi arutada.
Matemaatilised järjejutud noorte ajakirjades
Kuna mõlemas raamatus oli kirjanduse loetelus viiteid nii teistele raamatutele kui ajakirjadele, siis pisikese poisina linnas käies soetasin sealsest ajalehekioskist alati “Teaduse & tehnika” ajakirja (“Nauka i Zhizn“). Vene keelest aru ei saanud, aga igas numbris olid visuaalsed skeemid, koodinäited, ülesanded ja mängud.
Mõni neist suutis fantaasia lendu lasta. Näiteks venekeelses Noore Tehniku ajakirjas ilmus Mihhail Puhhovi sulest lausa ulmekirjanduse fännidele mõeldud järjejutt kuidas peategelane kosmoselaevaga seiklema läks ning kuidas igas numbris pidi ta siis mingit probleemi lahendama. Kord oli see koordinaatide süsteemis oma asukoha määramine. Kord tundmatul planeedil maandumine. Kord naasmine maa orbiidile.
Tublimad ülesannete lahendajad saatsid ajakirjale omapoolseid lahendusi ja programmijuppe, mida nood testisid, paremaid ära trükkisid ja kommenteerisid. DJVU failidena saab väljalõikeid neist ajakirjadest leida siit.
Mulle need seiklused väiksest peale väga meeldisid. Ja tõsiasi, et mõned nutikamad lahendajad osalesid aktiivselt lahenduste välja pakkumisel kirjeldab juba olukorda kus “playpen turns into playground” kui tsiteerida haridusgeeniuseid Marina Umaschi Bersi või Mitchel Resnickut. Mida arvate – kas see tänaste noorte puhul ka töötaks?
Üleskutse – palun mõtle kaasa:
Kirjeldasin enda kogemust, et kuidas mind noorena programmeeritavad taskuarvutid innustasid. Minu sisemise motivatsiooni käivitamiseks oli vaja:
- Avastamist väärt põnevat kalkulaatorit,
- Noortesõbralikke raamatuid ja ajakirju,
- Sõpru, kes samuti innustusid.
Palun jaga oma kogemusi. Ja mõtle kaasa, et mis võiks innustada sinu meelest tänaseid noori progemist või matemaatikat katsetama?
Kui tunned põhjalikumat huvi, võid lugeda veel edasi paari postscriptumit, mille hooga valmis kirjutasin, aga mis ülaltoodud mõtteavalduse sisule teistkordsel lugemisel palju juurde ei andnud. Ära ka ei raatsinud kustutada … 🙂
PS: Emulaatorid tänapäeval
PS. Post scriptum neile kes tahab nende kalkulaatorite kohta täpsemalt lugeda. Avastasin, et vene insenerid on võtnud minu kirjeldatud taskuarvuti järeltulijad MK 61 ja MK 54 ning kirjutanud neile toimiva emulaatori nii iPhone’i kui Androidi jaoks. Samuti on selle erinevad versioonid olemas online’is – näiteks siin ja siin.
Samuti on fännid kokku kogunud infot nii omaaegsete rakenduste kui ka lahenduste kohta. Mõned viited siin:
- Võimalus tõmmata alla neid ülaltoodud ajakirju ja emulaatoreid: http://www.emulator3000.org/c3.htm
- Siit võib alla laadida omale inglisekeelse kasutusjuhendi MK 61 jaoks.
- Programmeeritavate taskuarvutite fännileht Eggogoloogia
- Lühike inglisekeelne sissejuhatus: http://www.leningrad.su/b334/b334doce.htm
- Kuidas üks häkker Alfred Klomp on oma eesti sõbralt Sandrilt pärit MK61 häkkinud.
PPS: arvutamine võrdusmärgita?
Mis tegi B3-34 kalkulaatori eriti põnevaks oli võrdusmärgi puudumine!
Nimetatud põlvkonna arvutid kasutasid arvutustes pinusid. Tehnikaks oli arvutused esitada sulgudeta pöörkirje näol. Teisisõnu oli tegu tagurpidi-poola-kirjega (ma ei tea, et kas see on õige vaste “reverse polish notation” terminile, mille leiutajaks oli Poolast pärit teadlane Jan Lukasiewicz).
See sundis iga arvutust juba sisestamise käigus lihtsustama. Sulud tuli mõttes lahti punuda või kui tehete järjekord eeldas tagumise tehte esimesena sooritamist, siis arvutuste järjekord ja tehtemärgid tuli ümber mõtestada arvude sisestamise käigus:
Näide:
3 + 4 = asemel: 3 ↑ 4 +
3 − 4 + 5 = asemel: 3 ↑ 4 ↑ 5 - +
Sulgudega või tehete järjekorra arvestamisel läheb aga põnevaks:
(3 − 4) * 5 = asemel: 3 ↑ 4 - 5 *
3 − 4 * 5 = asemel: 3 ↑ 4 ↑ 5 * -Sulgude lahti punumine ja tehete järjekorra jälgimine arvutuse käigus oli ekstra mõtteharjutus. See sundis ka seostatumalt mõtlema, mis oli omakorda aluseks matemaatilise loogika kujunemisele. Sealt edasi on väiksem samm algoritmide aluste mõistmisele. Tingimuslaused (if … then … else) tuginevad samadel seostel. Tsüklid (while …, for …) eeldavad seoselist mõtlemist. Nimetatud teemad polnud tollal isegi kooli õppekavas. Aga nende mõistmine aitas omakorda jällegi algebrast või diskreetse matemaatika kontseptsioonidest paremini aru saada.
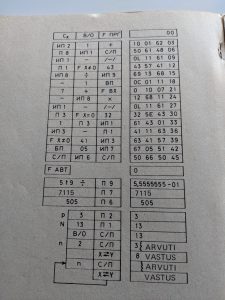
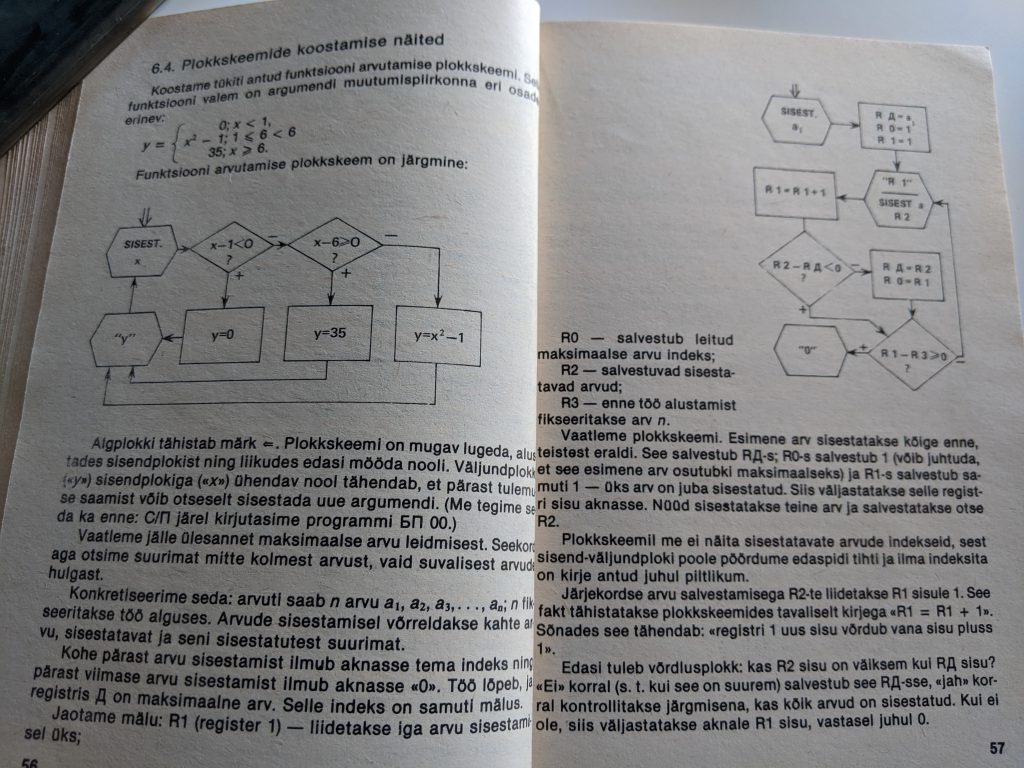
Niisiis – kõik see on sisuliselt süsteemse mõtlemise õppimine. Mis on millega seotud, kuidas neid seoseid saab erineval kujul kirjeldada, kujutada, selgitada ja mõtestada. Lisan siia veel mõned väljavõtted ka teisest raamatust (Slavin), kus ta kirjeldab pinude loogikat ja algebrade plokkskeeme noorele lugejale.